Fréchet mean

The Fréchet mean (named after Maurice Fréchet), is the point, x, that minimizes the Fréchet function, in cases where such a unique minimizer exists. The value at a point p, of the Fréchet function associated to a random point X on a complete metric space (M, d) is the expected squared distance from p to X. In particular, the Fréchet mean of a set of discrete random points x_i is the minimizer m of the weighted sum of squared distances from an arbitrary point to each point of positive probability (weight), assuming this minimizer is unique. In symbols:

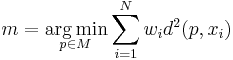$m = \operatorname{arg}\min_{\!\!\!\!\!\!\!\!\!\!\!\!\!\!p\in M} \sum_{i=1}^N w_i d^2(p,x_i)$ .

The name Karcher mean is sometimes used instead of "Fréchet mean", where this refers to Hermann Karcher.

1 Examples of Fréchet Means
2 Notes

Examples of Fréchet Means

Arithmetic mean

For real numbers, the arithmetic mean is a Fréchet mean, using as distance function the usual Euclidean distance.

Geometric mean

On the positive real numbers, the (hyperbolic) distance function 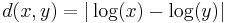$d(x,y)= | \log(x) - \log(y) |$ can be defined. 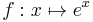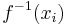The geometric mean is the corresponding Fréchet mean.Indeed $f:x\mapsto e^x$ is then an isometry from the euclidean space to this "hyperbolic" space and must respect the Fréchet mean: the Fréchet mean of the $x_i$ is the image by $f$ of the Fréchet mean (in the euclidean sense) of the $f^{-1}(x_i)$ , i.e. it must be:

$f(\frac{1}{n}\sum_{i=1}^n f^{-1}(x_i)))=\exp(\frac{1}{n}\sum_{i=1}^n\log x_i)=\sqrt[n]{x_1\cdots x_n}$ .

Harmonic mean

On the positive real numbers, the metric (distance function) 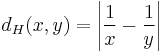$d_H(x,y) = \left| \frac{1}{x} - \frac{1}{y} \right|$ can be defined. The harmonic mean is the corresponding Fréchet mean.

Power means

Given a non-zero real number $m$ , the power mean can be obtained as a Fréchet mean by introducing the metric

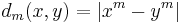$d_m(x,y)=| x^m - y^m |$ .

f-mean

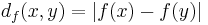Given an invertible function $f$ , the f-mean can be defined as the Fréchet mean obtained by using the metric $d_f(x,y)= | f(x)-f(y)|$ . This is sometimes called the Generalised f-mean or Quasi-arithmetic mean.

Weighted means

The general definition of the Fréchet mean that includes the possibility of weighting observations can be used to derive weighted versions for all of the above types of means.